Высшая математика: матрицы
rgrisshin 
Что такое матрица?
Матрица – это таблица элементов, каждый из которых характеризуется не только своим значением, но и местом расположения в таблице.
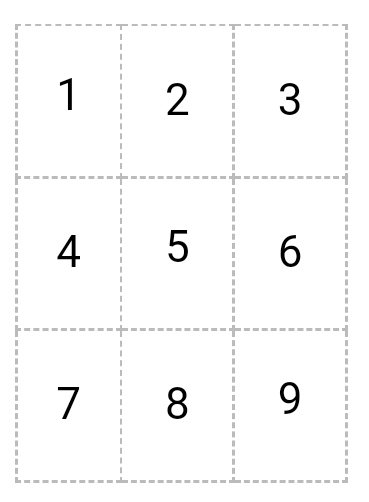
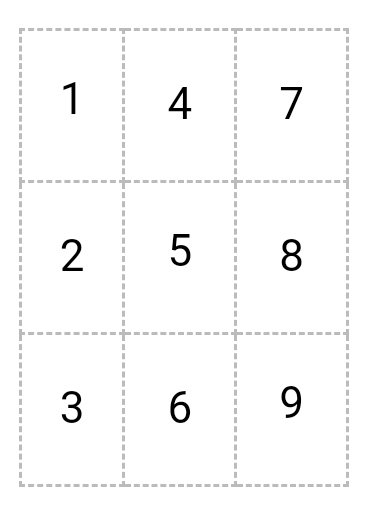
Пример (матрица 3*5):
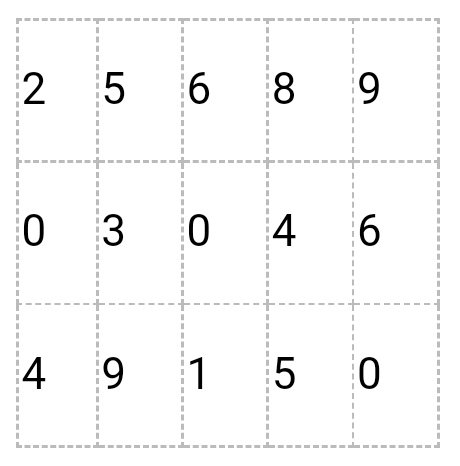
A (n*m), где n – число строк, а m – число столбцов.
A (n*n) – квадратная матрица
A (1*m) – матрица строка
A (n*1) – матрица столбец
Aij, где i – номер строки, а j – номер столбца.
Виды матриц
- Нулевая матрица
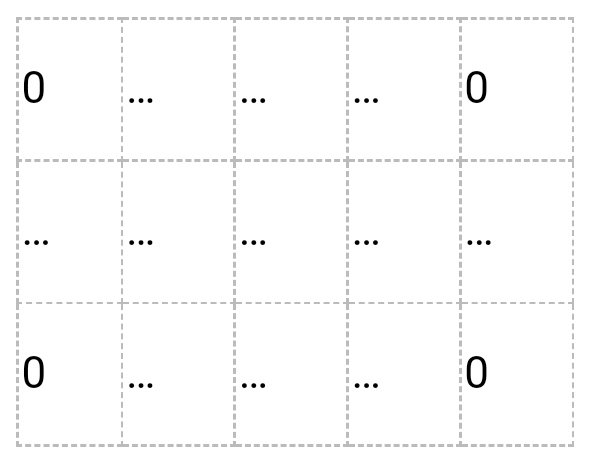
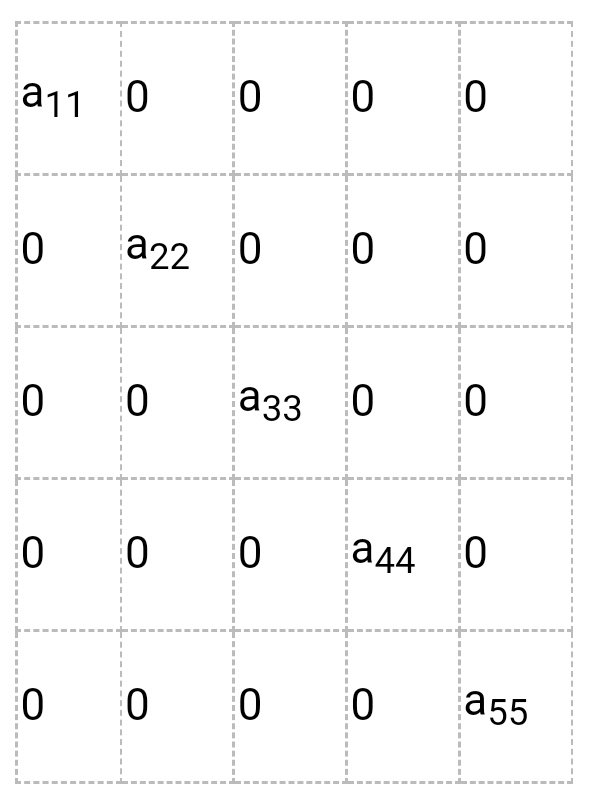
- Диагональная матрица
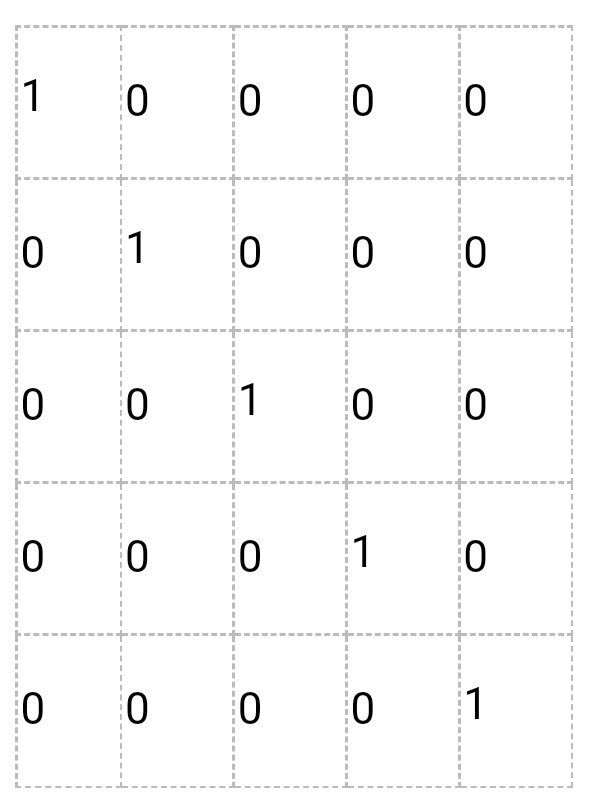
- Единичная матрица (E)
- Транспонированная матрица
AT = B
bij = aji
A =
AT =
При транспонировании строки и столбцы матрицы меняются местами.
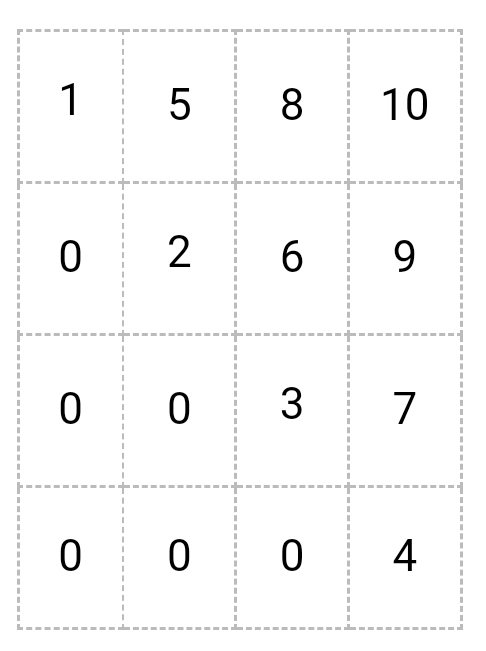
- Треугольная матрица
A =
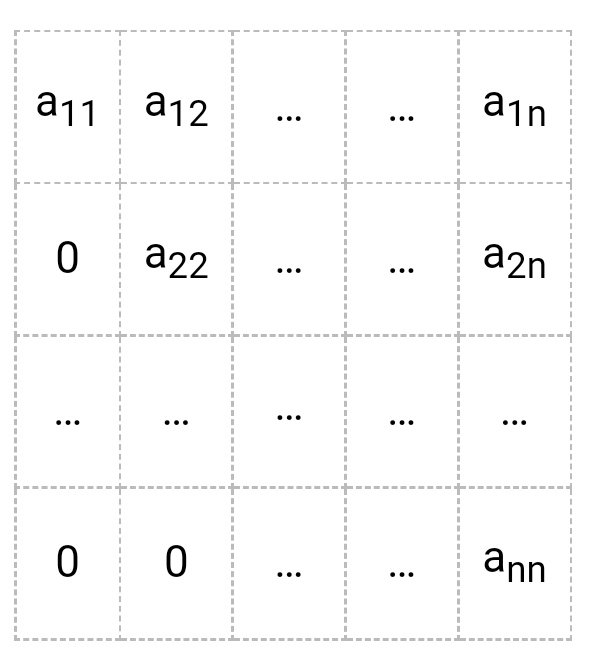
Пример:
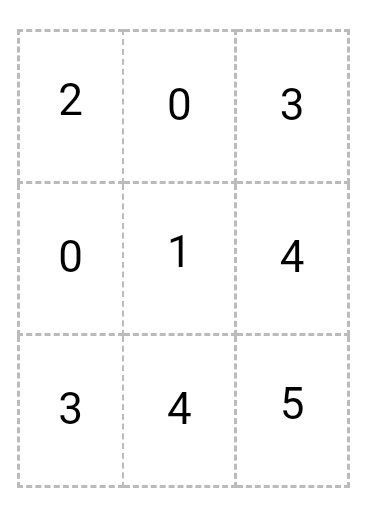
- Симметричная матрица
А (n*n) = ||aj||
aij = 0ji
A =
Свойства линейных операций с матрицами
- Коммутативность (перестановка)
A + B = B + A
A * α = α * A
- Ассоциативность (группировка)
(A + B) + C = A +(C + B)
- Дистрибутивность (управление)
(A + B) * α = α * A + α * B
Пример:
Найти f (A), если f (x) = 3x + 4
A =
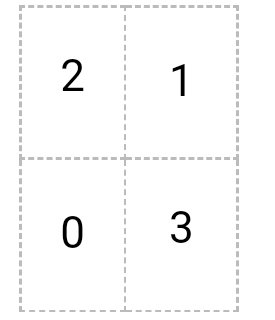
F (A) = 3 * A + 4 * E
(E – единичная матрица)
Нелинейные операции с матрицами
- Вычитание матриц
Пример:
Из матрицы
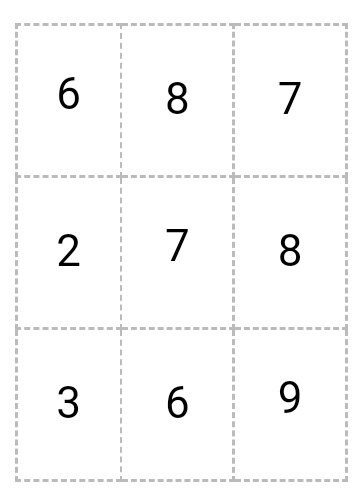
вычитаем матрицу
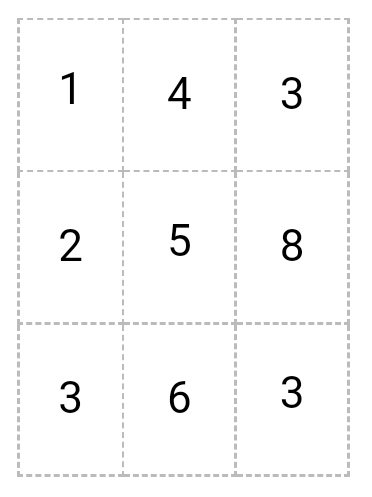
Получается
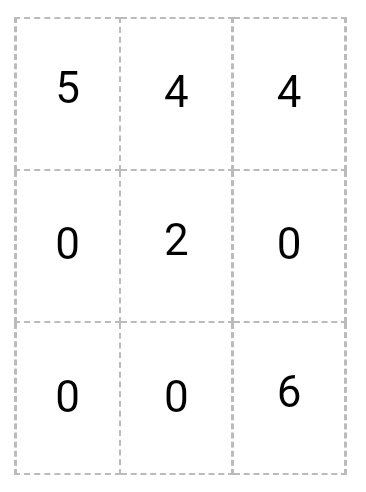
6 – 1 = 5
8 – 4 = 4
7 – 3 = 4
2 – 2 = 0
7 – 5 = 2
8 – 8 = 0
3 – 3 = 0
6 – 6 = 0
9 – 3 = 6
- Сложение матриц
Пример:
К матрице
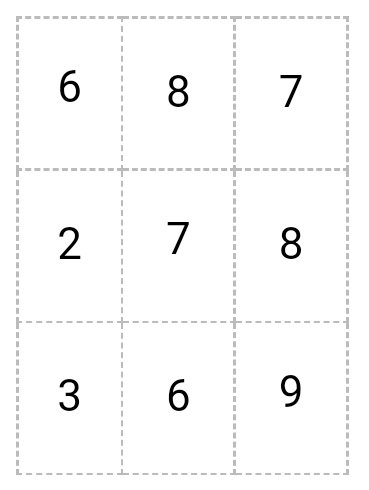
прибавляем матрицу
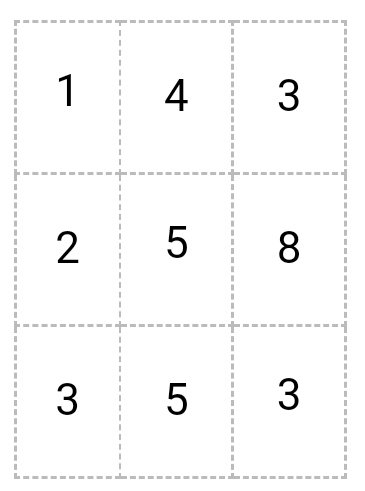
Получается
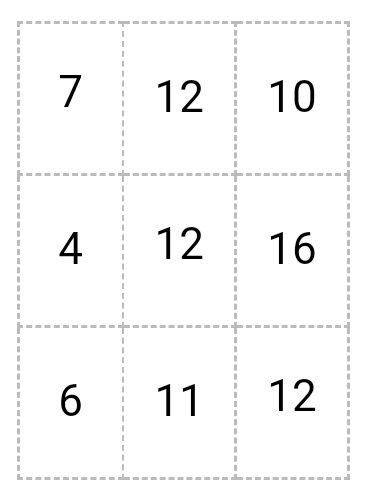
6 + 1 = 7
8 + 4 = 12
7 + 3 = 10
2 + 2 = 4
7 + 5 = 12
8 + 8 = 16
3 + 3 = 6
6 + 5 = 11
9 + 3 = 12
- Умножение матриц
Пример:
Матрицу
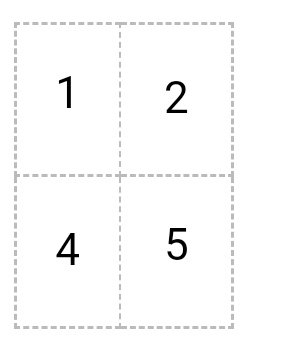
умножаем на матрицу
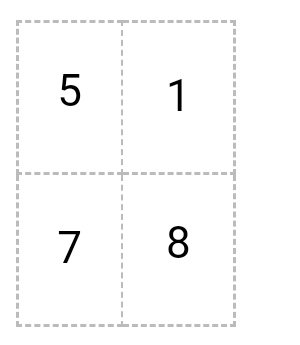
Получается
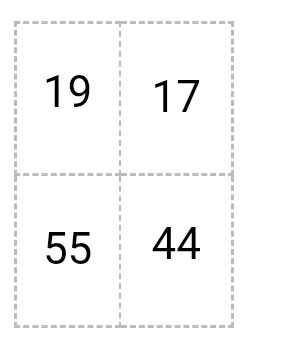
1 * 5 + 2 * 7 = 19
1 * 1 + 2 * 8 = 17
4 * 5 + 5 * 7 = 55
4 * 1 + 5 * 8 = 44
Похожие публикации
